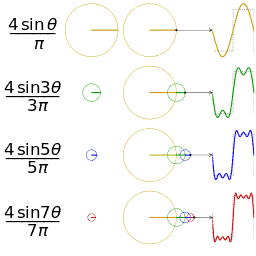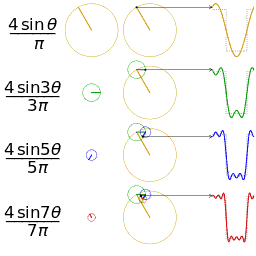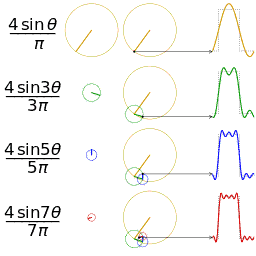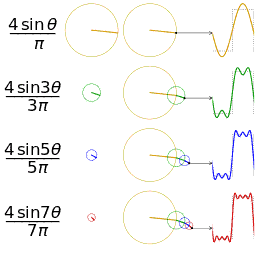Últimamente he visto varios proyectos en Kickstarter que prometían un osciloscopio digital con unos anchos de banda increíbles:
Los dos proyectos están basados en un núcleo digital realizado por una FPGA. Las FPGAs son dispositivos digitales de gran potencia, se pueden realizar combinaciones de puertas lógicas de forma muy sencilla y su precio ha ido disminuyendo hasta hacerlas muy accesibles, por todo esto han aumentado los proyectos realizados con estos dispositivos.
Una de las ventajas de las FPGAs es que se puede reutilizar el "código" (realmente no es un código tal y como se conoce en programación, sino más bien una configuración), de tal forma que se puede incluir los realizados por otra gente, lo que permite acelerar y simplificar aún más el proceso de desarrollo. Además se pueden paralelizar los procesos aumentando la capacidad de computación de forma espectacular, si esto lo combinamos con la potencia que actualmente tienen los PCs .
Sin embargo, existe un momento que debemos salir de la parte digital y enfrentarnos a la analógica y aquí es donde suelen empezar los problemas...
Supongamos que tenemos una frecuencia de muestreo de 1GSa/s, esto es lo mismo que decir que obtendremos muestras (de la resolución que sea) a la velocidad de 1GHz (1 millón de muestras cada segundo)...
¡Genial! ¡podemos ver señales de 1GHz! ERROR una señal (senoidal) de 1GHz quiere decir que cada ciclo dura 1ns (
=1/1GHz) pero es exactamente la cadencia con la que tomamos las muestras sólo tendríamos una muestra por cada ciclo, lo que es insuficiente para poder reconocer y reconstruir la señal (Caso A) .
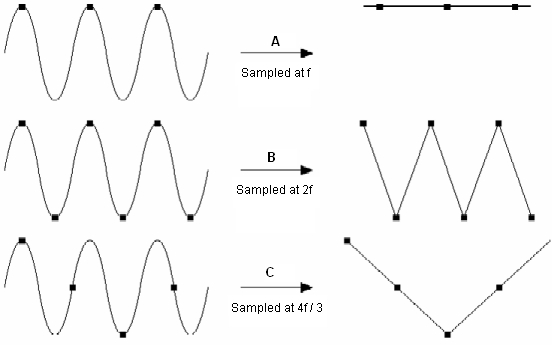 |
| Errores producidos por un muestreo insuficiente |
Si aumentamos disminuimos la frecuencia de entrada máxima permitida a 500MHz ya podríamos distinguir algo parecido a la señal deseada aunque no es exactamente lo que queremos (Caso B), pero ya estamos en el límite, con que disminuyamos un poco más la frecuencia ya se podrá reconstruir la señal de entrada (
Teorema de muestreo de Nyquist-Shannon).
Es decir, sólo con esto, hemos reducido el ancho de banda a menos de la mitad de la frecuencia de muestreo...
Pero estábamos hablando de señales senoidales, ¿qué pasa con el resto de señales?, bueno resulta que Fourier desarrolló una teoría matemática al respecto el "
Análisis armónico"; que, básicamente, dice que cualquier señal periódica puede descomponerse en ondas armónicas o senoidales (suma finita o infinita).
Por ejemplo, una señal cuadrada tiene infinitos armónicos, igual que una señal diente de sierra (todas las señales con discontinuidades o con derivada discontinua tienen serie infinita).
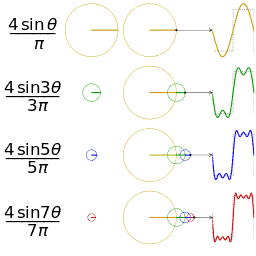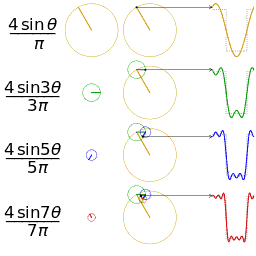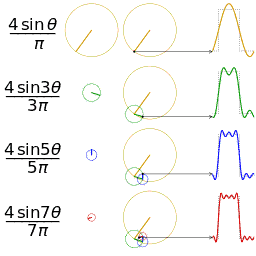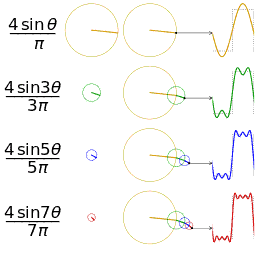 |
| 4 primeros armónicos de una señal cuadrada |
 |
| 5 primeros armónicos de una señal "diente de sierra" |
Esto quiere decir que no podríamos visualizar ninguna de estas señales (ya que el ancho de banda que necesitaríamos es infinito). Sin embargo, se puede ver que cada armónico lo que hace es refinar la función y tiene menor peso cada vez por lo que podemos despreciar los armónicos más altos (con peso muy pequeño en la señal final) y quedarnos sólo con los más bajos (con mayor peso en la señal final).
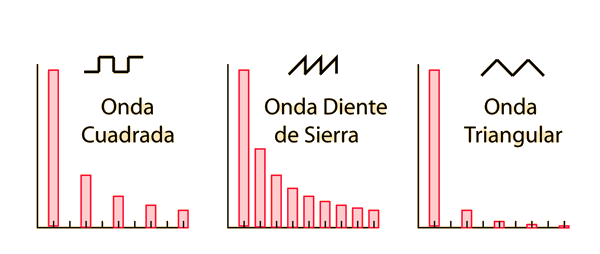 |
| Contribución de los armónicos a las señales Cuadrada, Diente de sierra y Triangular |
De esta forma consideraríamos que los armónicos mayores que 5f (dónde f es la frecuencia fundamental) despreciables.
De esta forma podemos decir que para 1GSa/s podríamos tener un ancho de banda de 100MHz dando un margen de 5f para los armónicos (contando que el teorema de Nyquist da un ancho de banda máximo de 500MHz).
Hay que decir que el margen de 5f es arbitrario, por ejemplo:
- Los RIGOL serie DS1000E tienen un 1GSa/s y un ancho de banda de 100MHz
- Los AGILENT serie DSOX2012A tiene 2GSa/s y un ancho de banda de 100MHz (aunque hay que decir que la serie llega a los 200MHz).
Por lo que se puede ver es una regla bastante usual en la industria. También significa que por cada ciclo tendremos un mínimo de 10 muestras.
Por ahora está bien, más adelante hablaré de cómo nos podemos saltar la restricción del teorema de Nysquist para aumentar el ancho de banda; y, por el contrario, qué beneficios tiene poner más muestras de las que tenemos (submuestreo y sobremuestreo).
S2
Ranganok Schahzaman
PD: sobre el primer link de kickstarter hay una discusión abierta en
reddit en el que lo sangran bastante, entre otras cosas por esto mismo que he explicado. Al final el creador ha tenido que reconocer que su ancho de banda no será de más de 5-10MHz.