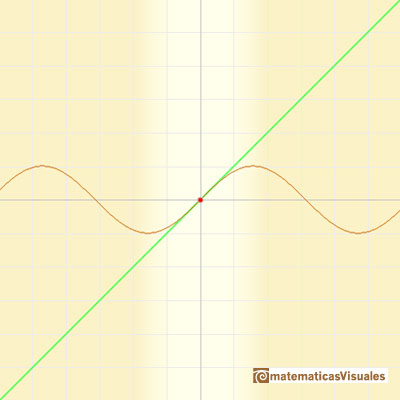
- El algoritmo utiliza una aproximación del valor devuelto por el accelerómetro tal que se considera sin(x) = x, esto se puede hacer a patir del desarrollo del polinomio de Taylor para esta función alrededor del ángulo 0:
$$ sin (x) = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + ...$$
Para un polinomio de grado 1, se puede observar que da una aproximación bastante buena para +-30º.
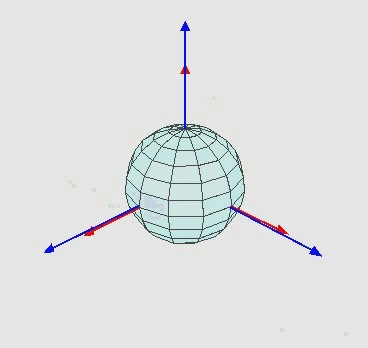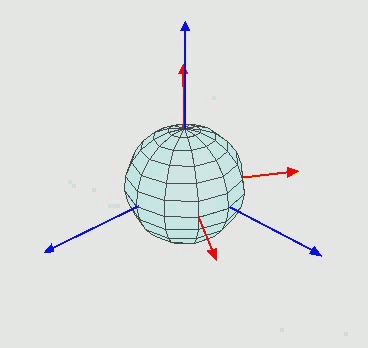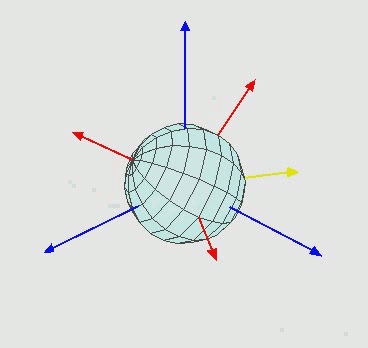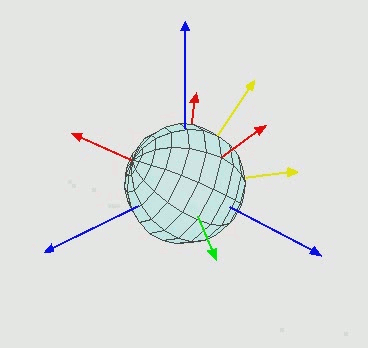
- En 3 dimensiones la cosa se complica ya que al girar uno de los ejes la rotación en los otros dos se ve afectada (por eso se dice que las rotaciones no son conmutativas, pero ya llegaremos a eso más adelante). Una imagen de la Wikipedia es mejor explicación:
Sin embargo el mismo algoritmo de filtros complementarios puede ser utilizado siempre que el desplazamiento del eje vertical no sea demasiado grande (mayor a 30º), de esta formas el accelerómetro corregirá este desplazamiento, aunque muy lentamente debido al filtro paso-bajo.
- La guiñada (yaw) no se podrá corregir con el accelerómetro (a no ser que este se ponga en uno de los extremos y podamos medir la acceleración centrípeta), por lo que sólo se corregirá a partir del giroscopio. el problema de esto es que el giroscopio presenta una deriva en el tiempo que hará que el sistema gire y no apunte a un rumbo concreto. Para corregir este giro deberíamos incluir un magnetrómetro en el sistema.
Fuente: http://www.matematicasvisuales.com/html/analisis/taylor/sinTaylor.html
No hay comentarios:
Publicar un comentario